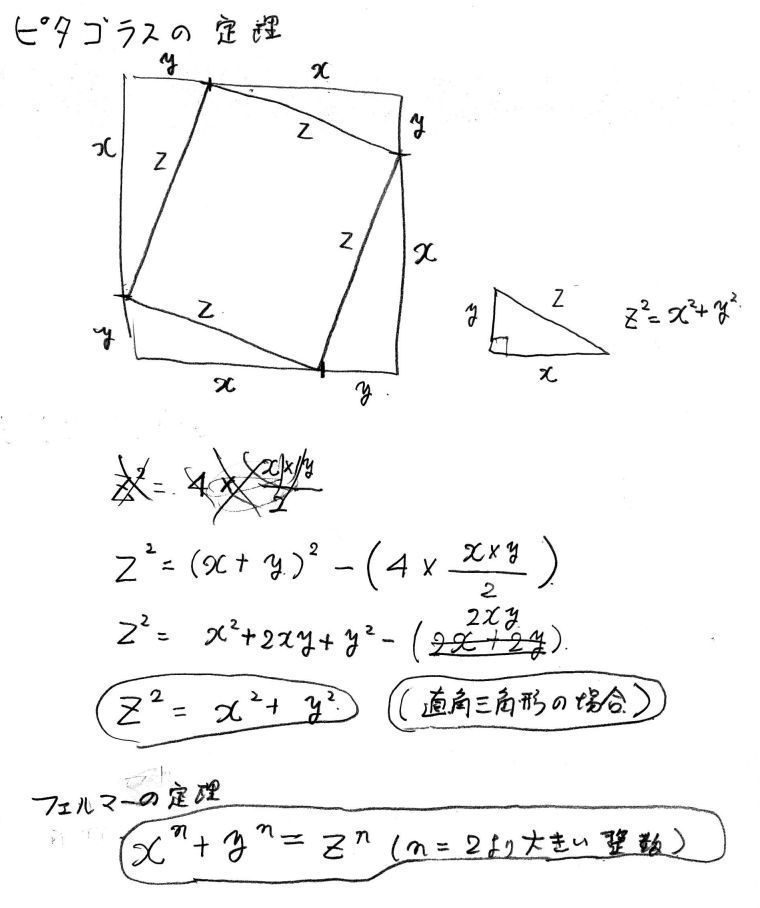
皆さん、ピュタゴラスはどのような人かは知らないけれど、
ピュタゴラスの定理は数学で聞いたことがあると思います。
実は小生、今、『フェルマーの最終定理 サイモン・シン著』という
数学ノンフィクション小説を読んでいます。
これが話の展開が非常に面白く、また、う~んと唸ってしまう真理や
数学の話が出てくるんです。
17世紀につくられた数学界最大の超難問”フェルマーの最終定理”を
数学者たちが3世紀に渡って挑戦する物語です。
その中で、著名な数学者の話があり、ピュタゴラスについても
超興味深い話が出てきます。
今回は、そのピュタゴラスの話を紹介します。
ピュタゴラスは、紀元前六世紀に生きた大数学者です。
ずいぶん昔の人ですね。
その頃、日本でいうと縄文時代なんです。
小説の一文を紹介とそれに対する小生のコメントです。
『ピュタゴラスの証明には反駁の余地がない。
彼の定理はこの世のすべての直角三角形において成り立つのである。
この発見の重大性にかんがみ、神々への感謝のしるしとして百頭の牡牛が
生贄に供されたといわれている。
この発見は数学における一つの里程標(物事の推移・発展の一過程を示すしるし)
であり、文明史的に見ても最大級の快挙といえるだろう。』
直角三角形の斜辺の二乗は、他の二辺の二乗の和に等しい。
何か、詩のような響きがありますね。
小生、中学3年生の時に習ったと思いますが、その時は何も感じませんでした。
(やっぱ、ただの平民なのでしょうね。)
今、考えると偉大な定理や法則は至ってシンプルで神がかっていると思います。
『ピュタゴラスの定理は二重の意味で重要だった。
第一に、これによって証明という概念が生み出されたこと。証明された数学的結論は、
論理を一歩一歩積み上げることで得られるという意味において、ほかのいかなる真
理よりも真である。』
ピタゴラスの定理は偉大ですが、意外と簡単に証明できます。
小生も昔を思い出してやってみました。
久々に自分は理数系出身だったことを思い出しました。
『ピュタゴラスの定理がもつ第二の重要性は、抽象的な数学の方法を具体的なものと
結びつけたことにある。ピュタゴラスは、数学的真理が科学の世界にも応用できることを
示し、科学に論理的な基礎を与えたのである。』
具体的に言うと、海王星は望遠鏡による観測の前に、数学的な計算によってその位置が予測され、
発見された惑星です。
現在では、スーパーコンピュータを使って、ほとんどの科学的事象を計算で導きすることが
できるんですよね。つまり、数値で事象を表しているということです。
良く数学は哲学であると言われますが、ある意味では白黒はっきりした
誰が考えても同じ答えが得られる人類最高峰の学問かもしれません。
今回、ピュタゴラスの素晴らしさが理解できました。
次に、フェルマーが待っています。
◆ホームページにお戻りの方が下記をクリックして下さい。
http://orinokasa.com/index.html
◆御意見をいただける方は下記 Commentをクリックして下さい。