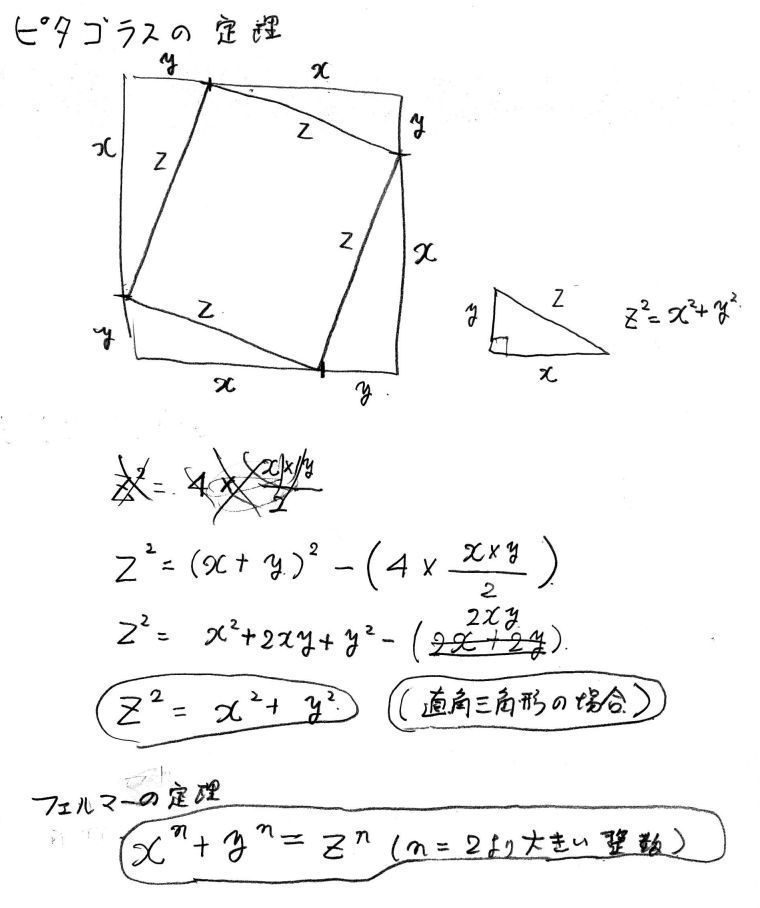
皆さん、先ず下記の手書きの数式を見て下さい。
2乗になっているのが、ピュタゴラスの定理
『直角三角形の斜辺の二乗は、他の二辺の二乗の和に等しい。』
ピタゴラスの定理は偉大ですが、意外と簡単に証明できます。
n乗になっているのが、フェルマーの最終定理
『nは2より大きい時、整数解はない』
nが2より大きくなっただけで、この定理の証明に数学者たちが
300年掛かったのです。
そのたいへんな偉業を『フェルマーの最終定理 サイモン・シン著』という
数学ノンフィクション小説が非常に興味深く書いています。
この小説は話の展開が非常に面白く、また、う~んと唸ってしまう真理や
数学の話が出てくるんです。
ただし、この超難問とされるフェルマーの最終定理を証明する目的は?
この小説には具体的には書かれていませんでした。
むしろ、フェルマーの最終定理の証明のみならば、なんの貢献度も
無いと言っています。
ただし、その証明に至るまでのありとあらゆる数学の定理を使用した
プロセスは数学界に最大の効果をもたらしたそうです。
また、数学的真理が科学の世界にも応用できることを示し、科学に論理的な
基礎を与えたとも言っています。
小生考えるに、この小説が我々に言いたかったことは2つ。
1つ目は、ものごとの真理を追究する場合、結果を重視する場合とそのプロセス
すなわち過程を重視する場合がある。
2つ目は、数学は誰が考えても同じ答えが得られる人類最高峰の学問である。
小生、この小説を読むのに、途中出てくる各種数学の定理を理解トライしながら
読み進めたので、多くの時間と少ししかない脳みそを使いきりました。
本件、小生の脳みその奥底に隠れていた数学の知識が、ぬかみそ樽の底に
沈んでいた萎れた茄子のように蘇りました。
さて、次は?
本棚に飾られている代数幾何学と微分積分学の教科書がこちらを見て
笑っています。
◆ホームページにお戻りの方が下記をクリックして下さい。
http://orinokasa.com/index.html
◆御意見をいただける方は下記 Commentをクリックして下さい。